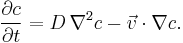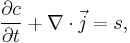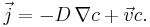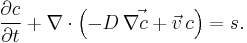Convection–diffusion equation
The convection–diffusion equation is a parabolic partial differential equation combining the diffusion equation and the advection equation, which describes physical phenomena where particles or energy (or other physical quantities) are transferred inside a physical system due to two processes: diffusion and convection. In its simplest form (when the diffusion coefficient and the convection velocity are constant and there are no sources or sinks) the equation takes the form: [1] [2][3]
The two terms on the right hand side represent different physical processes: the first corresponds to normal diffusion while the second describes convection or advection – which is why the equation is also known as the advection–diffusion equation. c is the variable of interest (species concentration for mass transfer, temperature for heat transfer), the constant D is the diffusivity for mass or heat transfer, and 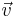 is the velocity.
is the velocity.
Stationary convection-diffusion equation refers to this same equation with the time derivative omitted.
Derivation
The convection–diffusion equation can be derived in a straightforward way from the continuity equation, which states that the rate of change for a scalar quantity in a differential control volume is given by flow and diffusion into and out of that part of the system along with any generation or consumption inside the control volume:
where 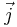 is the total flux and s is a net volumetric source for c. This flux can be written using the phenomenological Fick's first law, which assumes that the flux of the diffusing material relative to the bulk motion in any part of the system is proportional to the local concentration gradient. When there is convection or flow, the total flux in a stationary coordinate system is given by the sum of the diffusive flux in the material frame and what is known as the convective flux
is the total flux and s is a net volumetric source for c. This flux can be written using the phenomenological Fick's first law, which assumes that the flux of the diffusing material relative to the bulk motion in any part of the system is proportional to the local concentration gradient. When there is convection or flow, the total flux in a stationary coordinate system is given by the sum of the diffusive flux in the material frame and what is known as the convective flux 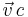 .
.
Combining these two terms the total flux becomes:
The substitution of this equation into the continuity equation gives the general form of the convection–diffusion equation:
In general, D, 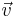 , and s may vary with space and time. In cases in which they depend on concentration as well, the equation becomes nonlinear, giving rise to many distinctive mixing phenomena such as Rayleigh–Bénard convection when
, and s may vary with space and time. In cases in which they depend on concentration as well, the equation becomes nonlinear, giving rise to many distinctive mixing phenomena such as Rayleigh–Bénard convection when 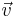 depends on temperature in the heat transfer formulation and reaction-diffusion pattern formation when s depends on concentration in the mass transfer formulation.
depends on temperature in the heat transfer formulation and reaction-diffusion pattern formation when s depends on concentration in the mass transfer formulation.
See also
References
- Granville Sewell, The Numerical Solution of Ordinary and Partial Differential Equations, Academic Press (1988). ISBN 0-12-637475-9